Stelling van Pythagoras: hoe werkt het?
De stelling van Pythagoras kan worden gebruikt om de zijden van een rechthoekige driehoek uit te rekenen.
Maar hoe doen we dit precies? Zie hier een voorbeeld en uitleg van Mr. Chadd!

Een rechthoekige driehoek is een driehoek met een hoek van 90 graden, zie onderstaande afbeelding. Het vierkantje geeft aan dat hoek C = 90°
Als een driehoek geen rechte hoek heeft (dus van 90°), dan kan de stelling van Pythagoras dus niet gebruikt worden voor die driehoek.
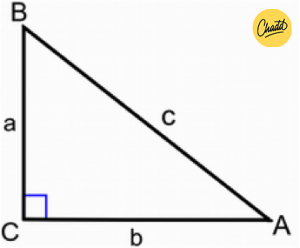
De stelling van Pythagoras is als volgt: a² + b² = c²
Hierbij geldt dat a en b de rechthoekszijden zijn (dus de zijden aan de rechte hoek) en c de schuine zijde. Dit is terug te zien in het plaatje. Als je de lengtes van 2 zijden van de driehoek weet, dan kan met behulp van de stelling van Pythagoras de derde zijde worden berekend.
Als er een tekening wordt gegeven, is het belangrijk om eerst te kijken of er een hoek van 90 graden in de driehoek is. Wanneer dat het geval is, moet je eerst vast stellen welke zijde a en b zijn (de rechthoekszijden) en welke zijde c is (de schuine zijde).
Wat betekent de term stelling van Pythagoras?
De stelling van Pythagoras is een wiskundige stelling die bedacht is door de Griekse wiskundige Pythagoras. ‘Zijn’ stelling was alleen niet nieuw voor de wereld, dat komt omdat in Soemer het resultaat al veel langer bekend was. Ook in Babylonië en het oude Egypte werd deze stelling al eerder toegepast.
Voorbeeld
Stel dat zijde a is 3 en zijde b is 4, zie onderstaande afbeelding.
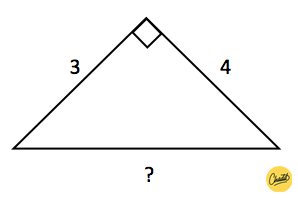
Dan geldt dus:
c² = 3² + 4² = 9 + 16 = 25.
Uit de stelling blijkt dus dat zijde c in het kwadraat 25 is. C is dus de wortel van 25, oftewel c is 5 (want √25 = 5).
Toch nog wat extra hulp nodig? Naast chatten met coaches kunnen ze jou ook bijles geven in wiskunde! Check deze pagina voor meer informatie.
Rechte hoek aantonen
De stelling van Pythagoras kan ook gebruikt worden om een rechte hoek aan te tonen. Als je alle zijden van de driehoek weet, maar je weet niet of een hoek 90 graden is, dan kan je dat controleren door te kijken of de stelling van Pythagoras geldt. Als het klopt dat a² + b² = c², dan heb je aangetoond dat de hoek inderdaad 90 graden is.
Samenvattend
Je kunt de schuine zijde van een rechthoekige driehoek berekenen met behulp van de Stelling van Pythagoras. Tevens kun je ook de rechthoekszijden van een driehoek berekenen met de Stelling van Pythagoras.
Mocht het toch nog niet helemaal duidelijk zijn? Stel dan je vraag bij Mr. Chadd! Onze slimme coaches helpen je graag verder!
Andere bezoekers keken ook naar: Hoe moet je afronden?
Leerlingen die hier vragen over hebben, keken ook naar:
Werkt u in het vo of mbo? Plan direct een vrijblijvende demonstratie in!
We laten u graag geheel vrijblijvend zien hoe Mr. Chadd werkt, hoe het kan worden ingezet en wat de meerwaarde is. Dit doen we in een fysieke of online afspraak van zo'n 30 minuten. Let op! Deze demonstratie is alleen bedoeld voor mensen die werkzaam zijn in het vo of mbo, NIET voor leerlingen!

Meer informatie over Mr. Chadd
Laat hieronder uw gegevens achter en we sturen u geheel vrijblijvend meer informatie over Mr. Chadd op!

Werkt u in het vo of mbo? Neem contact op!
Bent u benieuwd naar de voordelen van Mr. Chadd of heeft u andere vragen? Laat uw gegevens achter en wij nemen zo snel mogelijk contact op.


