Hoe werkt de stelling van Pythagoras eigenlijk?

Naast dat het al een hele kunst is om het correct te schrijven, is het ook goed om onder de knie te hebben hoe deze formule werkt. Daar gaat Mr. Chadd je mee helpen!

De stelling van Pythagoras kun je alleen gebruiken bij een driehoek waar één hoek in zit van 90 graden. Dit betekent dat de hoek loodrecht is. Met deze formule kun je de zijdes van een driehoek berekenen. De stelling van Pythagoras is a² + b² = c². Als je de lengte van twee zijdes hebt, blijft er dan nog een onbekende die je kunt uitrekenen via deze formule. De a en b in de formule zijn de zijde die aan de rechte hoek zitten. De c is de schuine zijde van de driehoek. Dit is ook te zien in figuur 1.

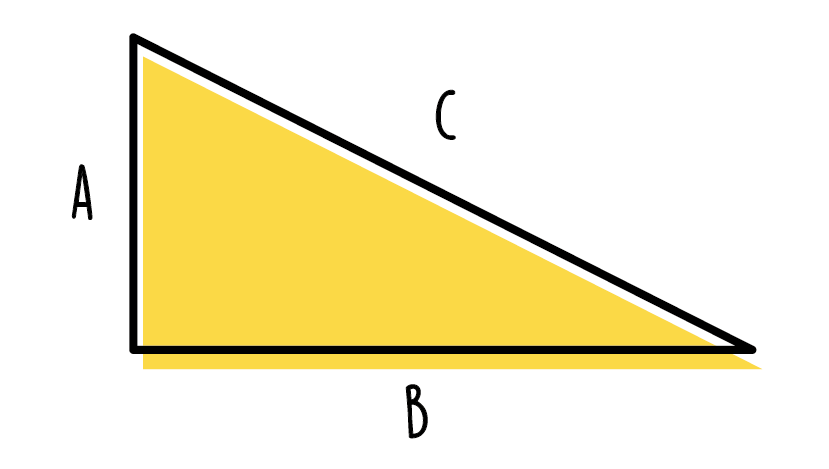
Figuur 1: Driehoek met een loodrechte hoek, waarbij de stelling van Pythagoras toegepast kan worden.

Hoe reken je met de stelling van Pythagoras?

In figuur 2 staat een driehoek met de zijdes AB, AC en BC. We weten de lengte van AC en BC, maar wat is de lengte van AB? Om dit op te lossen vul je eerst alle gegevens in in de formule. Je krijgt dan 7² + AB² = 10² . Vervolgens reken je de kwadraten uit. Dan krijg je 49 + AB² = 100. De volgende stap is alle getallen naar de rechterkant te halen en de letters naa de linkerkant, dat levert de formule: AB² = 100-49. Als laatste moet je alleen nog van beide kanten de wortel nemen zodat je AB te weten komt. Dan kom je uit op AB ≈ 7.14.

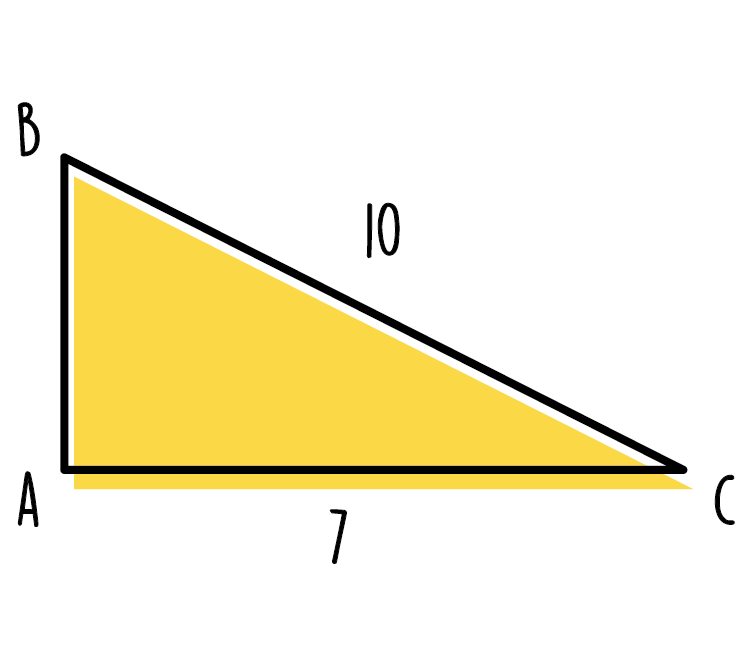
Figuur 2: Voorbeeld opgave stelling van pythagoras.

Oefenen met de stelling van Pythagoras? Maak dan de onderstaande oefenopgave.

1. De driehoek ABC heeft 3 zijden. Zijde AB is 10cm, Zijde AC is 5cm. Wat is de lengte van AB?
2. De driehoek XYZ heeft 3 zijdes, waarvan XY onbekend is. Zijde YZ is 13,5 cm en de zijde XZ is ook 13,5. Wat is de lengte van zijde XY?

Leerlingen die hier vragen over hebben, keken ook naar:

Stelling van Pythagoras: hoe werkt het?

Rechthoekige, gelijkzijdige- en gelijkbenige driehoeken

Sinus, cosinus en tangens: wanneer gebruik je welke?