Speltheorie
De speltheorie, vroeg of laat is dit een onderwerp die je ongetwijfeld tegen gaat komen bij economie.
Bij economie bestuderen we het keuzegedrag van de mens. Dit gaan we dus letterlijk bestuderen aan de hand van de speltheorie.
Welke keuze maken we precies wanneer? En waarom? Lees gauw verder en ontdek er alles over in dit artikel over speltheorie!

Wat je eigenlijk doet met de speltheorie, is het voorspellen van de uitkomst van een bepaalde keuze die gemaakt moet worden.
Er zijn vaak 2 partijen betrokken, ze moeten beide een keuze maken. De uitkomst van deze keuze hangt vaak samen met de keuze die de andere partij neemt. Vaak laat je de speltheorie zien aan de hand van een keuzematrix. Een voorbeeld van zo’n matrix vind je hier:

Je hebt dus in zo’n matrix te maken met 2 keuzes die de partijen individueel van elkaar kunnen maken. Wanneer A een keuze heeft die altijd het meest oplevert ongeacht waar B voor kiest, dan kun je dus voorspellen wat A gaat kiezen. Dit noem je de dominante strategie. De dominante strategie is de keuze die iemand maakt ongeacht de keuze van iemand anders. Het kan ook zo zijn dat er geen dominante strategie is, maar dit komt niet zo heel vaak voor.
Mocht je nou een evenwichtspunt hebben bereikt, waarbij het niet handig is voor één van de partijen om hiervan af te wijken, dan heb je het Nash-evenwicht te pakken. Zou één van de partijen wel afwijken, dan zal zijn beloning minder hoog zijn en dus is het niet aantrekkelijk om van het nash-evenwicht af te wijken. Een Nash-evenwicht is niet per se de beste uitkomst voor beide partijen. Als er bijvoorbeeld slechte communicatie is tussen de partijen dan kan het zijn dat niet de meest voordelige situatie gekozen wordt. Ook wanneer je bijvoorbeeld wel samenwerkt, maar er geen vertrouwen is tussen de partijen dan kun je op een evenwicht komen dat niet het meest voordelig is. Dit is het geval bij een gevangenendilemma , waarover je zometeen meer leest.
Een andere manier waarop de speltheorie toegepast kan worden is bij een sequentieel spel . Hierbij maken beide partijen niet tegelijk een beslissing, maar na elkaar. Om een sequentieel spel te voorspellen, heb je vaak een beslisboom nodig. Deze ziet er zo uit:
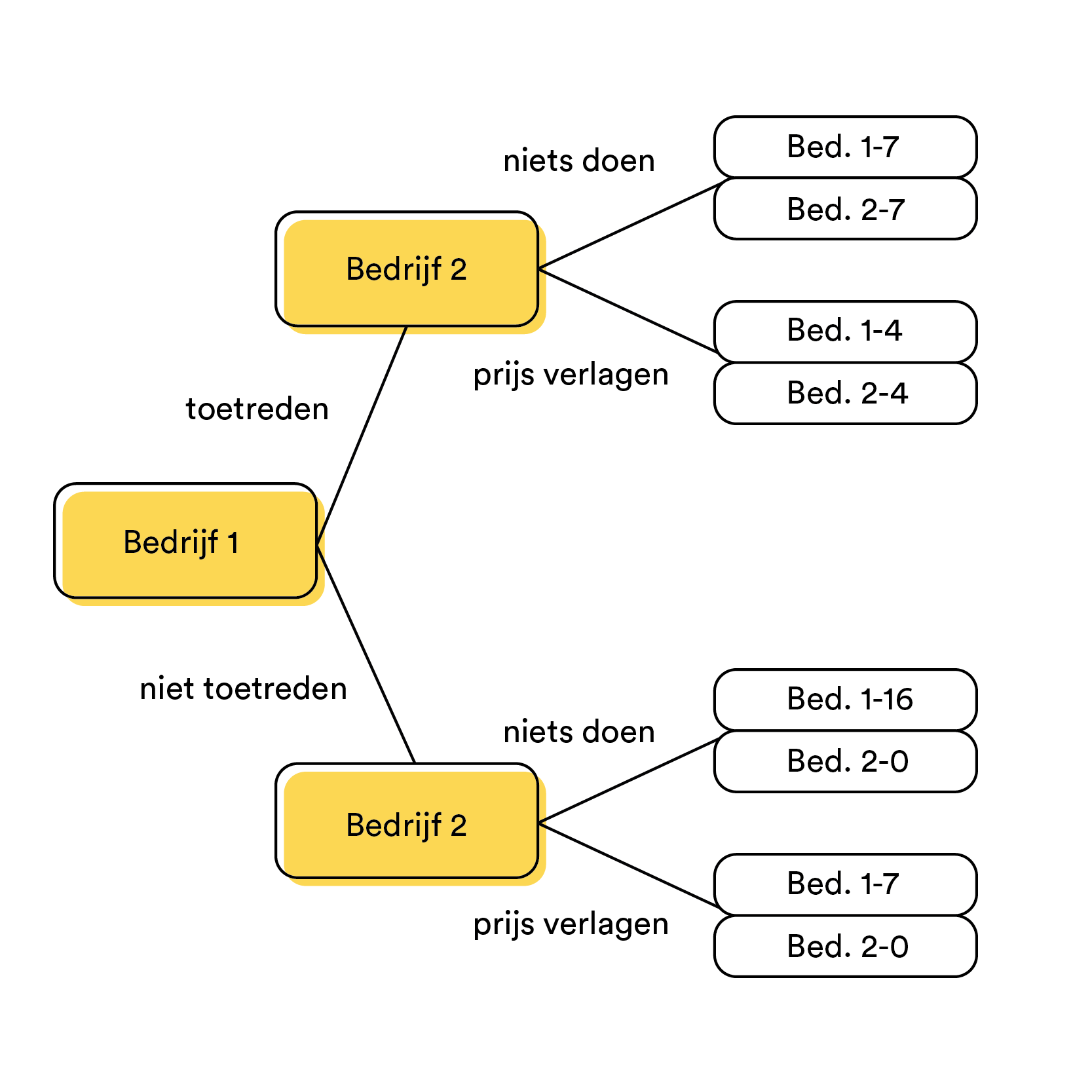
Doordat partijen na elkaar kiezen, kun je gaan voorspellen welke keuzes er gemaakt zullen worden.
Een toepassing van de speltheorie is het prisoners dilemma .
Hierbij ontstaat er een nash-evenwicht die niet optimaal is. En dit komt doordat er geen communicatie plaatsvindt tussen beide partijen. Zodra er communicatie mogelijk is, dan zou de uitkomst voor beide partijen de meest ideale zijn.
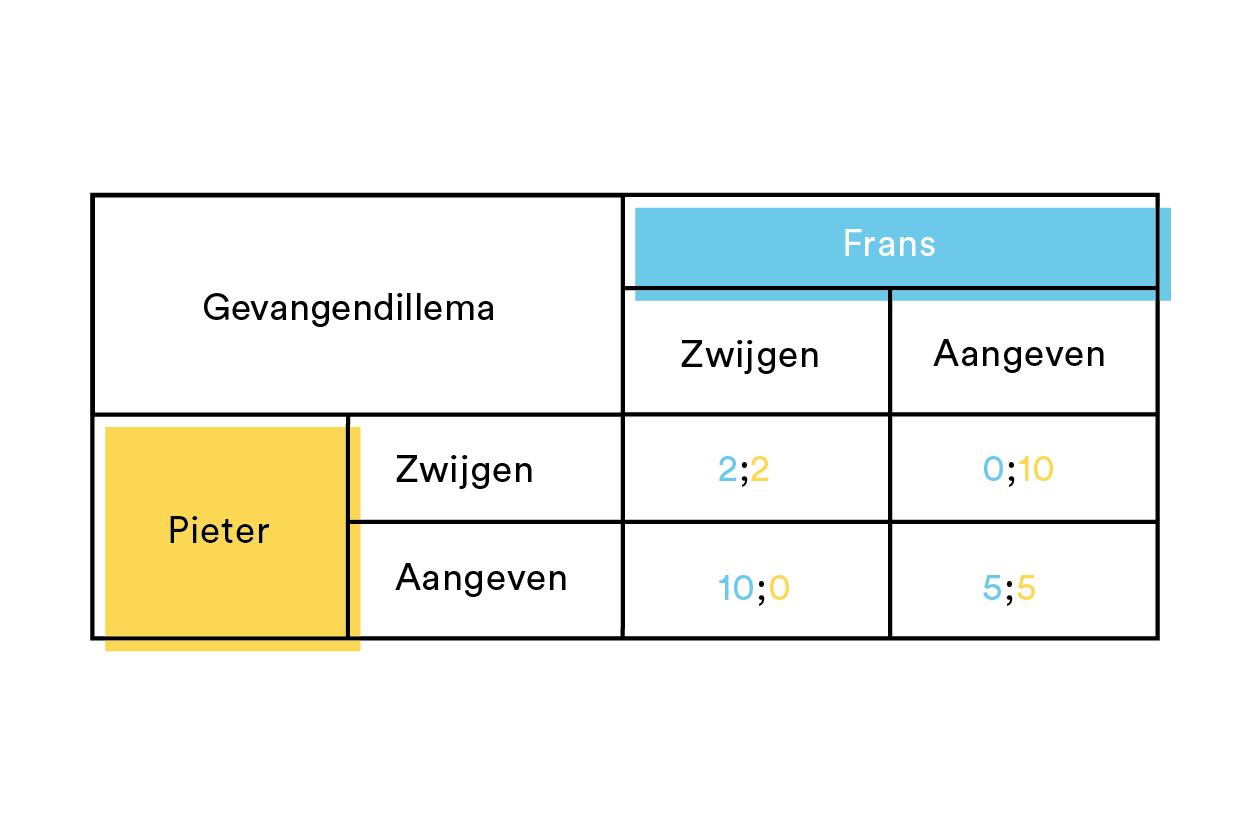
Laten we een letterlijk voorbeeld nemen: er is een moord gepleegd. Zowel Frans als Pieter hebben beide een wapen in bezit, en zijn dus verdacht. Als ze beide zwijgen dan krijgen beide partijen 2 jaar gevangenisstraf. Als één van beide de ander aangeeft en de ander zwijgt, dan krijgt degene die aangeeft vrijspraak en de zwijger 10 jaar. Geven ze beide elkaar aan, dan krijgen ze beide 5 jaar.
Nu komt de beslissing: als je zwijgt heb je kans op 2 jaar en op 10 jaar.
Als je de ander aangeeft heb je de kans op 0 jaar of op 5 jaar. Het is dus voor beide aantrekkelijker om de ander aan te geven, want in het ergste geval heb je dan 5 jaar. Nu komen we dus in de situatie waarbij beiden elkaar aangeven en dus beide 5 jaar krijgen. Als ze nou beide gezwegen hadden, dan hadden ze beide maar 2 jaar gekregen. Hier zie je dus dat het evenwicht dat bereikt wordt, niet de meest optimale situatie is. Dit komt omdat de gevangenen niet mogen overleggen. In een schema ziet deze beslissing er zo uit: (Hiervoor kunnen we het schema van het voorbeeld nemen maar dan vullen we de getallen, namen en acties in)
Herhaald spel: tit-for-tat strategie
Op het moment dat er telkens dezelfde keuze gemaakt moet worden dan is de kans groot dat een speler kiest voor een tit-for-tat strategie. Dit is te vergelijken met de uitdrukking ‘tand om tand, oog om oog’. Deze strategie is een beetje gebaseerd op het volgen van de andere speler. Stel je een markt waarbij er sprake is van dezelfde producten: het is een prijselastisch artikel.
Een aanbieder besluit nu voorzichtig zijn prijs iets te verhogen. De andere aanbieders besluiten mee te gaan, zodat het product overal wat duurder wordt. Mochten zij besluiten de prijzen niet te gaan verhogen, dan zal ook het bedrijf dat ermee begon, zijn prijs weer gaan verlagen. Zo zie je dus een soort van hele stille samenwerking: er is geen overleg, maar toch hebben elkaars keuzes invloed op elkaar. Dit is een voorbeeld van de tit-for-tat strategie!
Leerlingen die hier vragen over hebben, keken ook naar:
Werkt u in het vo of mbo? Plan direct een vrijblijvende demonstratie in!
We laten u graag geheel vrijblijvend zien hoe Mr. Chadd werkt, hoe het kan worden ingezet en wat de meerwaarde is. Dit doen we in een fysieke of online afspraak van zo'n 30 minuten. Let op! Deze demonstratie is alleen bedoeld voor mensen die werkzaam zijn in het vo of mbo, NIET voor leerlingen!

Meer informatie over Mr. Chadd
Laat hieronder uw gegevens achter en we sturen u geheel vrijblijvend meer informatie over Mr. Chadd op!

Werkt u in het vo of mbo? Neem contact op!
Bent u benieuwd naar de voordelen van Mr. Chadd of heeft u andere vragen? Laat uw gegevens achter en wij nemen zo snel mogelijk contact op.


