Differentiëren of de afgeleide berekenen is iets wat ontzettend vaak voorkomt in wiskundevragen en toetsen.

Ook voor je examen is het belangrijk dat je dit goed kunt. Maar hoe zorg je dat je differentiëren goed onder de knie krijgt?

Waarom moet je differentiëren?

Differentiëren wordt als heel belangrijk gezien, maar waarom precies? Als je een formule differentieert, dan bereken je de afgeleide. Deze heb je nodig om te bepalen of de grafiek in een bepaald punt van een grafiek stijgt, daalt of vlak is. Ook kun je hiermee bepalen hoe steil de helling van de grafiek is.

Hoe vind je de afgeleide van een functie?

De afgeleide van een functie vinden is niet altijd even makkelijk. Voor verschillende soorten formules, gebruik je verschillende methodes om de afgeleide te vinden. Wij bespreken hier de belangrijkste.

Basisregel

De belangrijkste regel om de afgeleide te vinden is de volgende:

Dit ziet er misschien heel ingewikkeld uit, maar dat valt eigenlijk wel mee. Wat je doet is de hele formule vermenigvuldigen met de macht (dit is n). Daarnaast haal je haal je van de macht 1 af, dat is de n-1.

Bijvoorbeeld: als je formule f (x) = 4x­­³ is, dan wordt de afgeleide f ‘(x) = 3f 4x3^-1 = 12x².* 
Deze kun je ook gebruiken als n een negatief getal is. Als* f*(*x*) = , bijvoorbeeld, dan kun je eerst omschrijven naar* f*(*x*) =* x^-2 * en vervolgens de basisregel toepassen. Je krijgt dan:* f ‘(x) = –*2*x^-2-1 = –*2*x^-3.* 

Afgeleide van andere functies
Soms moet je de afgeleide vinden van een andere functie, zoals bijvoorbeeld f(x) = sin(x). De belangrijkste andere functies staan hieronder aangegeven, deze moet je uit je hoofd leren, want je krijgt deze niet op je examen.

Somregel
Als je formule f(x) = g(x) + h(x) is, dan kun je de afgeleide vinden door f’(x) = g’(x) + h’(x) toe te passen. Je neemt dus de afgeleiden van de losse stukjes en telt deze bij elkaar op. Bijvoorbeeld: als f(x) = sin(x) + x² , dan wordt f ‘(x) = cos(x) + 2x.

Productregel
Soms wil je de afgeleide berekenen van 2 functies die met elkaar vermenigvuldigd zijn. In dat geval moet je de productregel toepassen. Deze gaat als volgt:

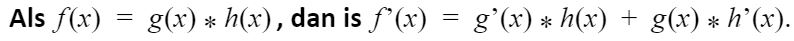
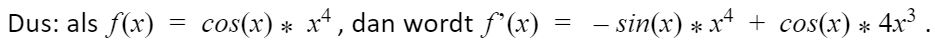
Quotiëntregel

De quotiëntregel gebruik je als je een functie hebt waarbij je een functie hebt die uit een breuk tussen twee functies bestaat. De quotiëntregel gebruik je als volgt:

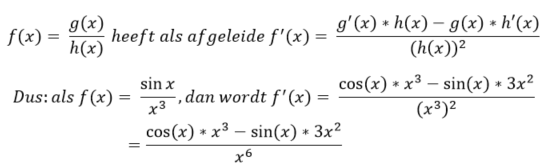
Kettingregel

De kettingregel gebruik je bij lastigere formules. Kijk hiervoor bij dit artikel .

Leerlingen die hier vragen over hebben, keken ook naar:

Kettingregel

Machten

Hoe los je wortelvergelijkingen op?